Generation and reversal of the geomagnetic field as a part of the global geodynamic process
S. S. Tsygankov (II), S. S. Tsygankov (III)
26 December 2017
SUMMARY
The paper attempts to explain the generation and cyclic alternation of the magnetic field sign based on the hydromagnetic dynamo theory within the framework of global geodynamic model. The main physical processes of the model are surface cooling of the initially molten body and internal radiogenic heating. It is shown, that during crystallization, accompanied by the contraction, and heating, occurring with the dilatation, the Earth’s radius experiences cyclic changes (decrease and increase, respectively). This leads to the creation of a difference in the rotational velocities of the solid outer shell (mantle) and the liquid core. This results in the formation of oppositely directed vortex flows of an electrically conducting fluid. According to the hydromagnetic dynamo theory this leads to the geomagnetic field generation and alternation in its sign depending on whether the mantle rotates faster than the core (a direct field) or the core rotates faster than the mantle (a reversal field). The geomagnetic field reversal is shown to be one of the natural consequence of the global geodynamic process.
Key words: Structure of the Earth – Geomechanics – Earth rotation variations – Fracture and flow – Geomagnetic induction – Reversals: process, time scale, magnetostratigraphy.
1 INTRODUCTION
The reversal of the magnetic field is one of the main problems of the Earth sciences. Numerous field studies have established a sequence of oppositely directed magnetization of lava and sedimentary rocks (Gaffin 1989; Merrill et al. 1998; McElhinny and McFadden 2000). Four epochs over the past 4.5 million years can be distinguished: Brunhes, Matuyama, Gauss and Hilbert. More detailed analysis revealed shorter polar reversals during these epoches. Reversal of the Earth’s magnetic field was discovered in even more ancient volcanic and sedimentary rocks. The frequency of reversals did not remain constant during the evolution of the Earth. Analysis of the time scale of geomagnetic polarity alternations revealed the prevalence of the reverse polarity during the Riphean epoch. Starting from the early Paleozoic and up to date an increase of the direct polarity contribution is observed with increasing frequency of the field polarity reversals (Pechersky 1997; Petrova 2002).
The paper attempts to explain the cyclic alternation of the magnetic field sign based on the hypothesis of hydrodynamic dynamo in the framework of geodynamic model of the Earth. Particularly, we consider two main physical processes: cooling from surface of the originally molten planet and internal radiogenic heating (energy sources, however, may be different during the Earth evolution) (Romashov and Tsygankov 1996; Tsygankov et al. 2003; Tsygankov 2006; Tsygankov 2009).
2 ON THE MECHANISM OF THE MAGNETIC FIELD GENERATION
The predominance of the dipole field component and its axial direction indicate that the geomagnetic field is associated with the rotation of the Earth (Kosygin and Maslov 1989; Bobryakov et al. 1991). It is also supported by the correlation between the Solar system planets rotational velocities and values of their magnetic moments (Hubbard 1984; Marov 1986). For slowly rotating planets (e.g., Mercury and Venus) the magnetic moment is about one ten-thousandth from the Earth’s one. For the fast rotating Jupiter and Saturn it is several orders of magnitude larger. The relationship between the magnetic field strength and the planet’s rotational velocity is evident also from the observed correlation between variations of these quantities (Kalinin and Kisilev 1978). In particular, periods of the geomagnetic dipole variations (66.7; 33.3 and 21.4 years) coincide with the periods of changes in the Earth’s rotation rate (Braginsky 1982).
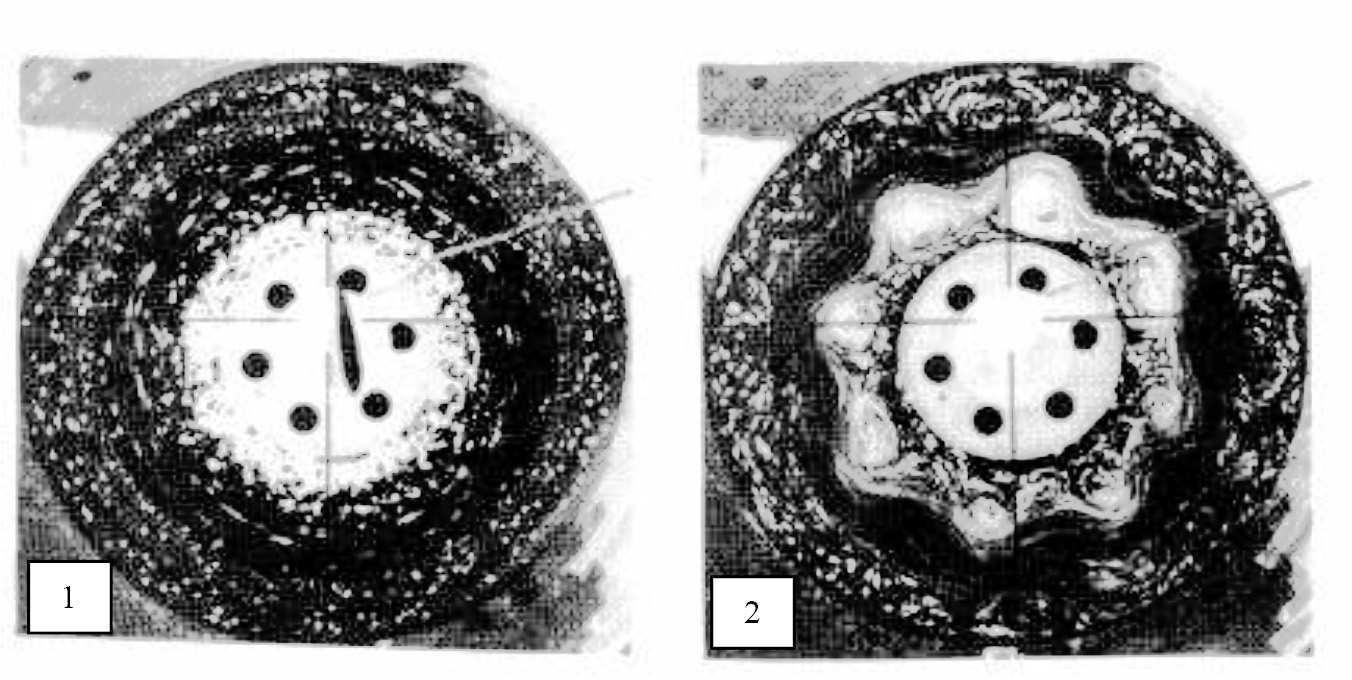
Figure 1. The results of the vortex motion generation modeling: track pictures of the (1) subcritical and (2) supercritical rotating fluid flows. The appearance of a regular vortex pattern is seen in the latter case. From Dolzhansky and Manin (1993).
However, it is obvious that rotation only is not sufficient to generate a magnetic field. It requires either some ordered motion of electric charges inside the interior or the relative motion of matter possessing the electromagnetic properties (Bobryakov et al. 1991). The possibility of the free charges presence at the border between mantle and core, which are significantly different in their electrical properties, under high pressure and other conditions inherent to the deep structures of the Earth, was shown by e.g. Vorobiev (1980). The next problem is related to the directed motion of the matter inside the Earth. The results of modeling the formation of vortex structures in a rotating fluid are shown in Figure 1 (Dolzhansky and Manin 1993; Krymov 1987).
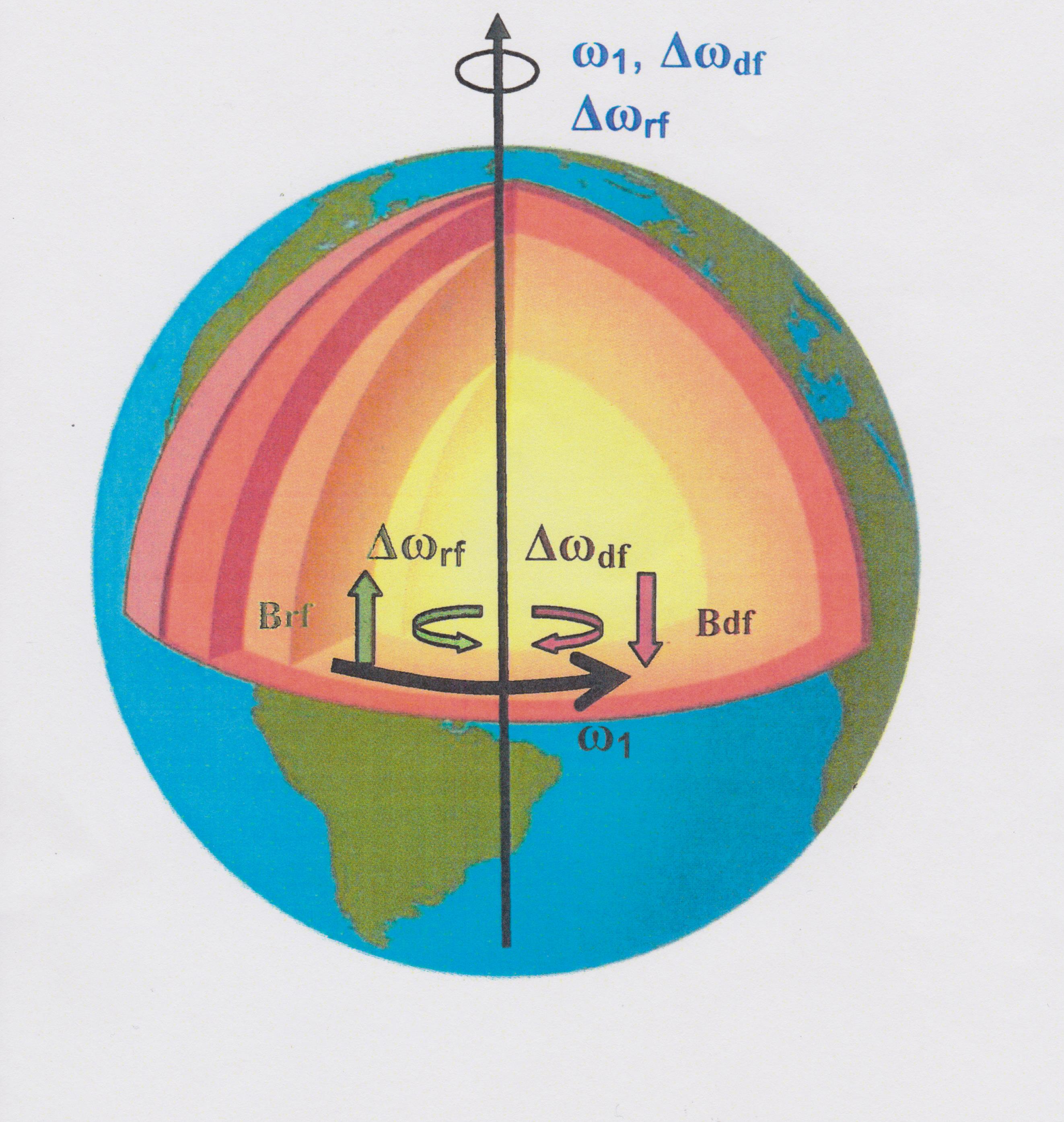
Figure 2. Scheme of rotation of geospheres: ω_1 – angular velocity of Earth rotation; ∆ω_df – direction of the speed of rotation of the outer core relative to the mantle (westward drift), creating a direct magnetic field B_df ; ∆ω_rf is the direction of the speed of rotation of the outer core relative to the mantle, which creates a magnetic field of the opposite direction B_rf .
Another well established geophysical fact is a westward drift of the Earth magnetic field lines with velocity of about 0.2 angular degree per year (Zharkov 1983). Taking into account that magnetic field is generated in the liquid core, from this one can assume that for the generation of the magnetic field the rotation of the conductive material of liquid core relative to the mantle is required (Orlenok 2000). At the border of these two significantly different in their physical properties structures the formation of electrical charges is possible. Their rotatory motion leads to the formation of the magnetic field (see Figure 2) (Dobretsov et al. 2000).
The difference between the rotational velocities of the liquid core and it’s internal and external boundaries (the inner core and the mantle) is evident from another geophysical data as well (Avsyuk 1996). Gradient of physical and mechanical properties of the liquid core material with depth (in particular, viscosity by 4-5 orders of magnitude (Letnikov 2001)) causes its mechanical stratification. In addition to the formation of the main differential rotation it causes formation of thin boundary layers with conditions for the generation of the vortex motions (see Figures 1 and 3). This results in generation of two types of the magnetic field different in size and power – main and boundary dynamo. For compatibility of the fluid motion at the layers boundaries, the directions of these motions there must be opposite (Figure 3). Accordingly, they will create a magnetic field of the opposite signs.
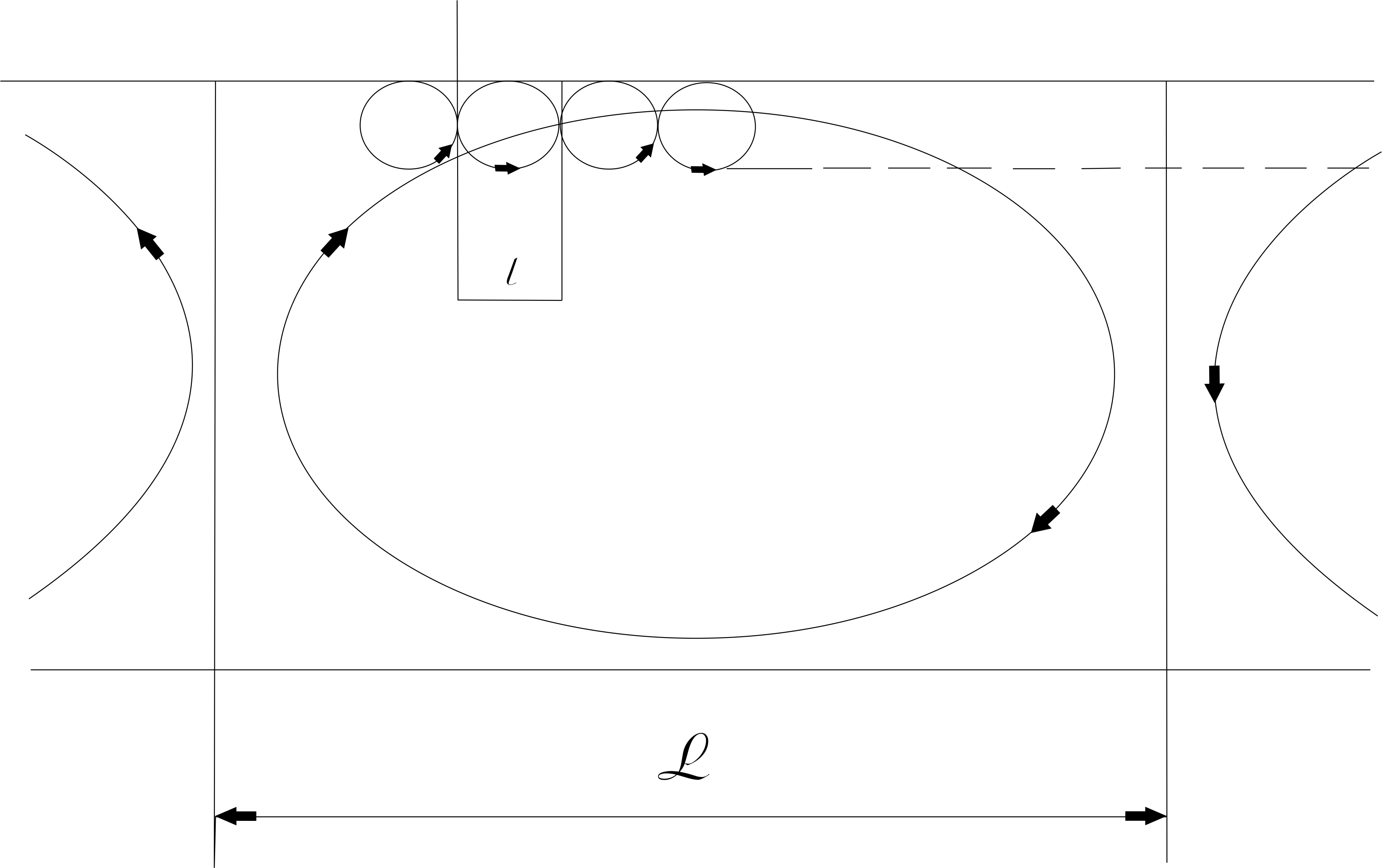
Figure 3. Relationship of the large- and small-scale convective structures in a liquid nonequilibrium layer with different in depth viscosity properties (sectional view). The effect was studied experimentally and was shown to persist with a complication of geometry of the nonequilibrium layer from flat to cylindrical and spherical ones (Petrov and Movchan 2003).
The magnitude of the induced magnetic field is determined by the velocity ∆ω of the outer core rotation (“rotor”) with respect to the Earth’s mantle (“stator”). Viscous friction on the border between mantle and core will cause an equalisation of the rotor and stator velocities (∆ω → 0). As a result the rotational motions will be damped leading to the field decay and sharp reduction of the field strength.
Generation of the magnetic field with opposite direction can be associated with a change in the sign of the relative rotational velocity between outer core and the mantle and, therefore, with the formation of main and frontier dynamos with another direction of the conductive material flows in the outer core.
Thus, the generation of the magnetic field may be associated with different angular velocities of rotation of the mantle and the liquid core, when either the mantle rotates faster than core (direct field) or core rotates faster than mantle (reverse field). Then it is necessary to find a mechanism redistributing the angular momentum within the Earth’s body in order to explain the reversals of the magnetic field.
3 ON THE GEODYNAMIC MODEL OF THE EARTH
The analysis of geodynamic processes and their energetics shows that two main physical processes underlie the evolution of the Earth: external cooling from the surface and internal heating. The relative contribution of energy sources was different throughout the Earth’s evolution (Lyubimova 1968; Smyslov 1979; Bott 1974; Scheidegger 1982; Zharkov 1983). We assume that initially the Earth was molten. This follows from the estimates of the energetics of processes taking place at early stages of the Earth evolution: the collision of planetesimals during accretion onto the planet, differentiation and compression of matter, decay of short-lived radioactive elements, etc. (Ringwood 1966; Wetherill 1972; Windley 1975). This is evidenced by the absence of geological data on the first half billion years of the planet’s life. Then the liquid-to-solid phase transition, going with the volume shrinkage during its crystallization and cooling from the surface from one side, and internal heating, going with the increase in volume, from another, are the two main physical process cyclically changing the radius of the Earth, and, respectively, geometric and inertial characteristics of the outer and inner shells.
Formation of solid outer shells during crystallization causes changes in the thermodynamic states of the planet, i.e. alternation of cooling and heating predominance. During the epoch of the volume shrinkage due to crystallization of the internal matter the radius is reduced. During the expansion epochs radius is increasing due to inner material effused to the surface (Romashov and Tsygankov 1996). Variations of the radius in time can be approximated by a sine curve with varying amplitude.
The maximal amplitudes of the radius variations can be estimated from analysis of the local vertical squeezings of internal matter at the Earth’s surface appeared through the faults formed during the period of the shell tension. The mechanical load-bearing capacity of the damaged mantle will be restored when the difference between the internal pressure, which led to the destruction, will be balanced by the weight of vertical heaves γ × ∆H, where γ – specific weight, ∆H – height of the heave. Considering the Mohr-Coulomb criterion as equation of the strength and assuming shell thickness of 700 km (the maximum depth of the earthquakes), γ = 3 × 104 N/m-3 and the angle of internal friction of 30^o , using equations from Nadai (1969) one can get ∆H about 20 km. This roughly corresponds to the maximum amplitude of the height differences at the Earths surface (from –8000 up to +9000 m).
4 ON THE MECHANISM OF THE REVERSAL OF THE GEOMAGNETIC FIELD
As it follows from the geodynamic model the increase and decrease of the planet’s radius alternate in time. Due to conservation of angular momentum these changes of the radius cause the relative motion of the conductive liquid core with respect to the mantle. Moreover, the motion of two types is possible: the mantle outpaces the outer core or vise versa, creating direct and reversal magnetic field, correspondingly (Figure 2).
Suppose the whole planet, consisting of the mantle of the radius R 1 (I in Figure 4a), liquid outer core of the radius R 2 (II in Figure 4a) and the inner solid core of the radius R 3 (III in Figure 4a), rotates with a constant angular velocity ω_0 (big arrow in Figure 4a or blue line 1 in Figure 4b). The change of the rotation velocity of mantle and core during the expansion phase of the internal substance leading to the formation of the reversal field is shown schematically in Figure 4. Suppose also that the processes of the outer shell destruction and magma squeezing through the cracks (1 in Figure 4a) are resulting in the uniform increases of the planets radius by ∆R. In this case the axial moment of the mantle C_M is increased by ∆C_M , accordingly. Based on the law of conservation of angular momentum, it will lead to a decrease in the angular velocity of the mantle by ∆ω = ω_0 (∆C_M /(C_M + ∆C_M)). This is relative velocity of the outer and inner cores with respect to the mantle (arrows in Figure 4a and solid red line 2 in Figure 4b).
The rotational motion of charged particles in the liquid core will create a magnetic field. The total magnetic dipole moment of the entire liquid core (P_m) can be obtained by integrating of the magnetic moments of individual currents over the whole core’s volume. If we assume that charges are uniformly distributed over the volume then
Pm=4π/15[R15+R25–R12 x R22 x (R1+R2)] x n x e x Δω (1)
where n is the number of charges per unit volume, e - the charge (Yavorsky and Detlaf 1977).
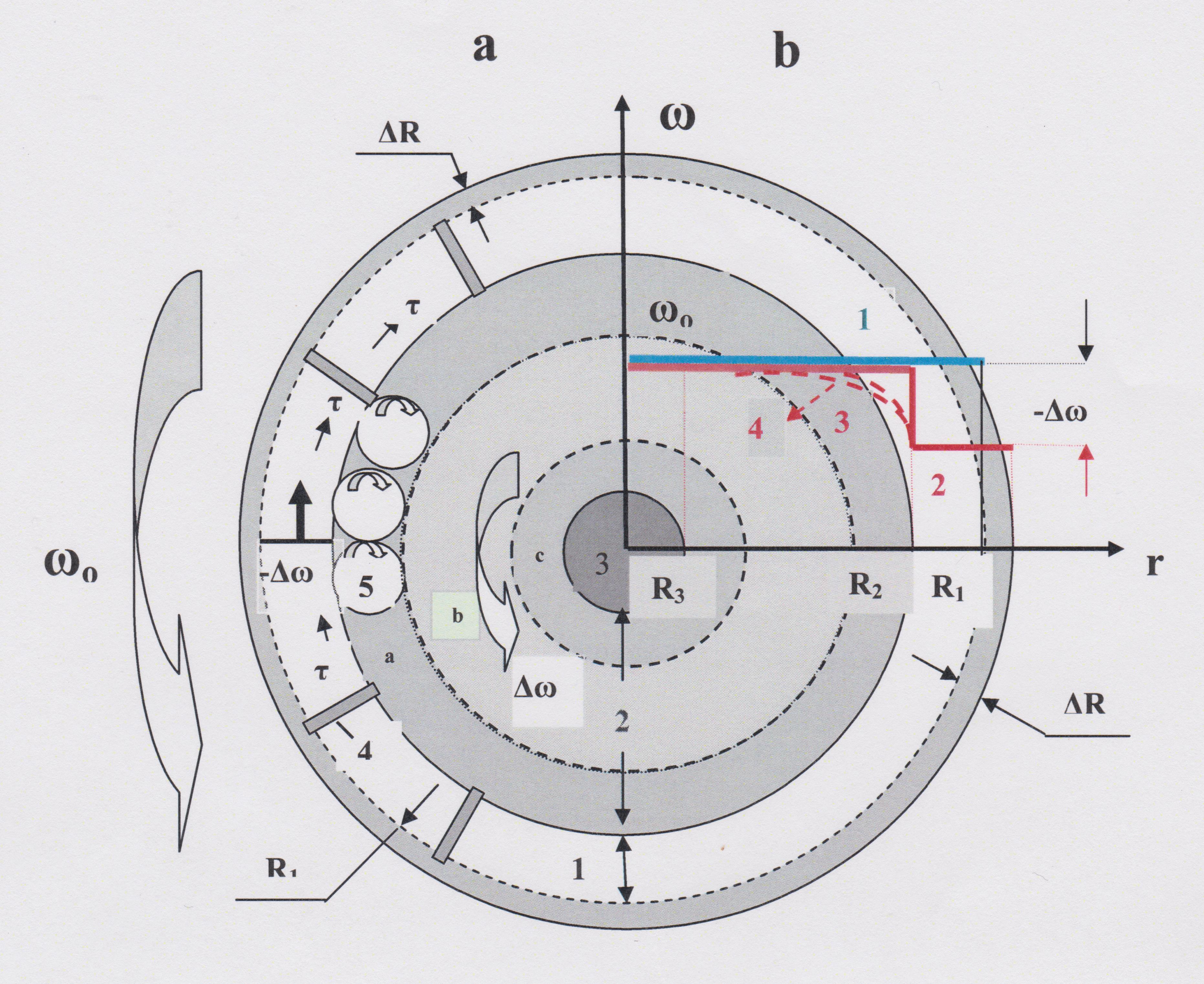
Figure 4. a) The scheme of the model of the reversal field formation (not on a scale): I – mantle (R_1 – radius); II – outer core (R_2 – radius; a, c – frontier shells with the vortex motion of matter; b – the main cranking of liquid substrate); III – the inner core (R_3 – radius); 1 – faults – channels of squeezing of internal substance; 2 – vortex cell; ω_0 – initial speed of rotation of the planet; R_1 – the initial radius of the Earth; ∆R – increase of the planet’s radius at the expense of the inner substance effused; ∆ω – the relative rotational speed of the liquid core with respect to the mantle; τ – force of viscous friction; b) Distribution of angular velocity of rotation of shells of the Earth: ω_0 – initial speed of rotation of the whole planet (blue solid 1). With a decrease in the angular velocity of rotation of the mantle (−∆ω) due to an increase in the radius of the planet (+∆R) (red solid line 2); red dashed line 3 – the qualitative distribution of the angular velocity of rotation of the outer core after time ∆t, resulted from the motion of the deceleration front (red arrow 4).
The difference in the rotational velocities at the border between mantle and outer core results in the viscous force τ = η∆ω (where η is the viscosity) directed against the cranking of the core (Figure 4a). At the same time the deceleration front (arrow 4 in Figure 4b) will start to develop from mantle into the core with a rate dependent on the dynamic viscosity of the matter. Qualitative distribution of the the rotation velocity after time ∆t is shown with red dashed line 3 in Figure 4b. The released rotational energy is converted into the heat (this is one of the possible sources of internal energy) (Letnikov 2001).
The difference between the rotational velocities of the mantle and liquid core with huge gradient in the viscosity properties would lead to the stratification of liquid core. Besides the formation of the main crank (zone IIb in Figure 4a), additional vortex cells (2 in Figure 4a) are formed at the boundaries of the liquid core (zone IIa in Figure 4a) similar to structures observed in experiments shown in Figures 1 and 3. Alignment of the matter motion at boundary of vortex cells with the main crank requires an opposite directions of these motions. It results in the different directions of the magnetic field induced in the main and frontier dynamos. The decreasing strength of the main dipole due to the reduced relative angular velocity ∆ω, will become equal with the field strength generated in the boundary areas. Given their different signs it would lead to fluctuations in the magnetic field direction. This is consistent with the facts that as the magnetic moment decreases at the beginning of the reversal, an increase number of excursions is observed (Braginsky 1987).
After the deceleration wave (red arrow 4 in Figure 4b) reaches the surface between liquid and solid cores, the difference in the rotational velocities of the outer and the inner cores appears (Levin 1996; Tkalčić et al. 2013). It makes possible the formation of another boundary region with a circular motion of the matter (IIc in Figure 4a). This leads to the situation when three main geospheres (mantle, outer and inner cores) are rotating with different angular velocities, which is observed at present time. At some point the velocities will be equalized due to friction until the next unbalance of the angular moments will occur, etc. At the present time the geomagnetic field is well approximated by a central dipole and 8 radial components, located on the border of the inner and outer cores (Avsyuk 1996). Figure 1 shows the results of simulations of the appearance of such flows.
A similar processes (but with the opposite direction of the matter motion in the core) take place during the shrinking of the internal volume. Decrease of the Earth radius would increase the angular velocity of the mantle and change the direction of matter flow in the outer core, and, consequently, result in the change of the magnetic field direction.
Generation of the oppositely directed liquid flows is confirmed by studies of the spherical Couette flows (shear flow of viscous incompressible fluid in a spherical shell with boundaries rotating around the same axis with constant but different angular velocities). It was shown that the motion of the fluid consists of the “primary flow” around the rotational axis and the “secondary flow”, type and structure of which depend on three parameters: Reynolds number Re_1 = 2ω_1 r_1/ν, relative layer thickness δ = (r_1 − r_2 )/r_2 and the Rossby number ε = (ω_1 − ω_2 )/ω_2 , where ω_1 and ω_2 – angular velocity of the external and internal spheres, respectively; r_1 and r_2 – external
and internal radii of the spheres, respectively; ν – kinematic viscosity (Josef 1976; Munson 1975; Yavorska et al. 1977; Yavorska et al. 1978).
Figure 5a shows the lines of equal angular velocity (left) and current lines of the secondary flow (right) for r_2 /r_1 = 0.5 and Re = 100 in the case of the fixed outer sphere (ω_1 = 0), and the inner sphere rotating relative to it. When the inner sphere is fixed (ω_2 = 0) and the outer sphere rotates, the secondary flow is reversed.
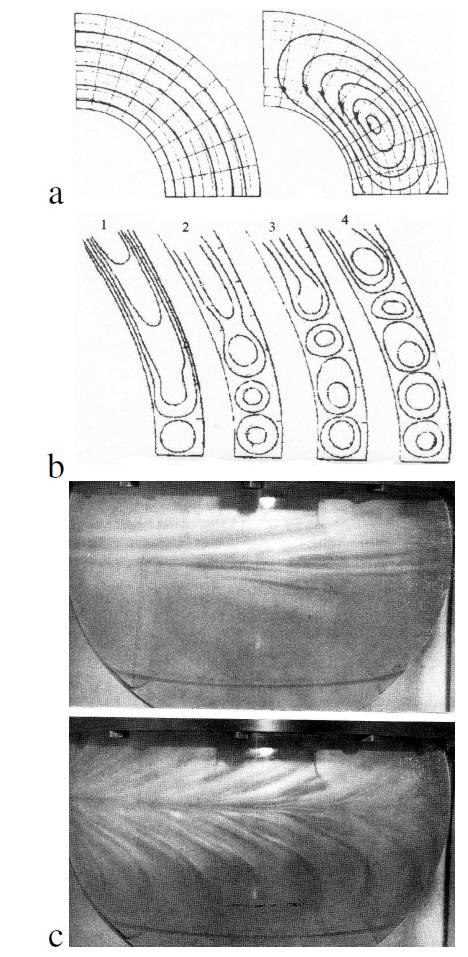
Figure 5. a) The lines of equal angular velocity and current lines of the secondary flow for r_2 /r_1 = 0.5, Re=100 and ω_1 =0 (outer sphere is fixed) (Josef 1976); b) the current lines of the secondary flow in the layer δ=0.11 for different values of Re: 1 – 1270; 2 – 1600; 3 – 1900; 4 – 2300 (Yavorska et al. 1978); c) images of secondary flows in a thin layer (Yavorska et al. 1977).
It was shown experimentally that at high Reynolds numbers different phenomena associated with the formation of boundary and shear layers become significant. Then various vortex structures can be formed in thing layers (Figure 5b). Depending on the similarity parameters, secondary flow is three-dimensional and has a spiral form, which structure depends on the direction of rotation of the outer sphere (Figure 5c). These results confirm qualitatively the model assumptions on the possibility of various types of flows between two rotating with different angular velocities shells. They also show an opposite direction of these motions depending on which sphere rotates faster – inner or outer one.
The cyclic increase and decrease of the mantle radius R_1 on the value (∆R) changes its momentum of inertia. Based on the law of conservation of angular momentum this creates a difference in the relative angular velocities of core and mantle
Δω/ω0≈1-[(1-n5)/(1-n3)]x[(1-n3+3(ΔR/R_1))/(1-n5+5(ΔR/R_1))], (2)
where n = R_2/R_1 – ratio of the radii of the outer core and the planet.
As can be seen from eq. (2), the relative rotational velocity ∆ω depends on the absolute velocity of the planet’s rotation ω. Slowly rotating planet would have low maximal cranking velocity of the core ∆ω. This may be a cause of the weak magnetic fields at Mercury and Venus, possessing rotational periods significantly longer than the Earth one: 58.6 and 243.2 days, respectively. In a more general case, the dependence of the magnetic moment on the spin period is observed for the other planets of the Solar system (see Figure 6) (Hubbard 1984).
Figure 6 clearly shows that planet 4 (Mars) significantly deviates from the general correlation of the magnetic moment on the planet’s spin period. According to the latest data it’s magnetic field is defined by the residual magnetization of the rocks only and dynamo does not work for already about two billion years. Based on the proposed model, this is due to the fact that the cooling process on Mars went much more intensively than on Earth because of smaller size and larger distant from the Sun. At a certain historical stage liquid core has solidified (R_2 = R_3; see eq. (1)) and the process of the magnetic field generation has stopped (P_m = 0).
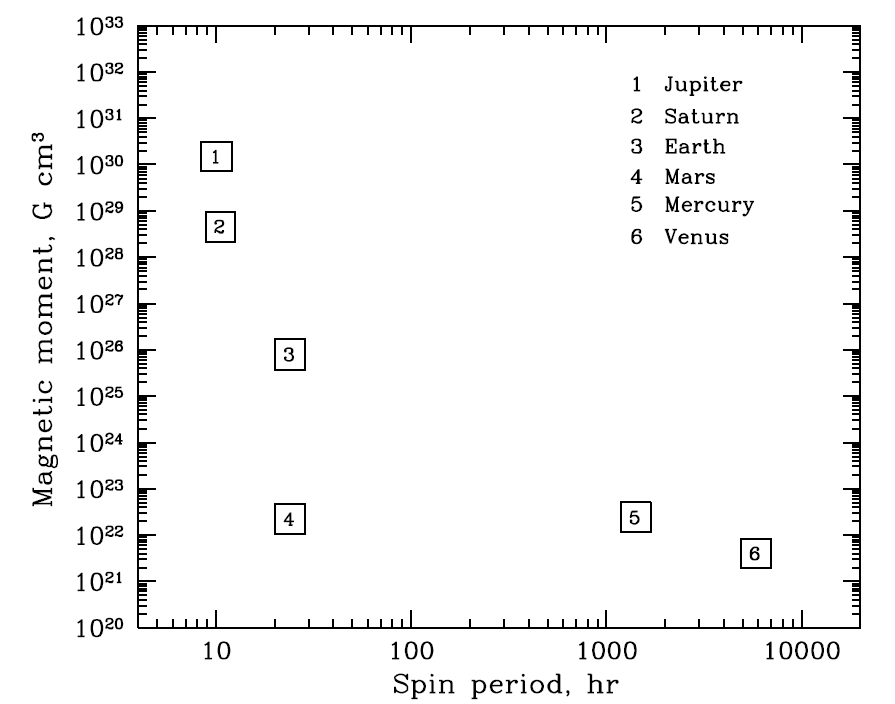
Figure 6. The dependence of the magnetic moment P m [G cm^3 ] on the planet’s spin period T [hr]: Jupiter (1), Saturn (2), Earth (3), Mars (4), Mercury (5), Venus (6).
From observations of the westward drift one can estimate the relative velocity of the core cranking relative to the mantle of ∆ω ∼ −3.5 × 10^−3 y^−1 (lags behind) (Orlenok 2000; Zharkov 1983). According to the equation (2) such relative rotation could arise due to the change in average radius of the Earth by only 10 m. During the planet history the crystallization front has reached a depth of 2900 km. Taking the relative volume shrinkage (∆V /V ) of 3% this could lead to a decrease in the radius of about 45 km. If a 10 m radius change is sufficient to inverse the geomagnetic field, about 4500 reversals have occurred over 4.5 billion years. This corresponds to about 1 million years lifetime of a field of one sign, which agrees with the observational data (Orlenok 2000).
According to the geological data, the rate of the plumes effusions over the last 50 million years is 2 × 10^6 km^3 My^−1 (Dobretsov et al. 2005). Assuming the same rate of the effusions in the past and the fact that they took place all over the planet’s surface, uniformly increasing its size, this gives an average increase in the radius of 5 m My^−1 and frequency of reversal every 2 million years. It is seen that various estimates of the average frequency of reversals and observational data are of the same order.
5 ON THE CONNECTION BETWEEN MAGNETIC FIELD INVERSION WITH OTHER PROCESSES IN THE GEO- AND BIOSPHERES
The proposed model predicts a close relationship between the cyclical processes of the Earth’s crust destruction with the reversals of the magnetic field. From the available data it is necessary to note the coincidence of the long epochs (160-200 My (Petrova 2002)) of stable geomagnetic field with the Bertrand geodynamic cycles (150-250 My (Khain 2000; Khain 2003)). Moreover, these periods coincide with climatic cycles associated with volcanic activity, also reflecting geodynamic activity (Chumakov 2001). Studies of the relationship between the geomagnetic field reversals on the one hand, and geodynamic manifestations (plumes) and changes in the organic world over 370 million years on the other, showed that these phenomena are really close to be synchronous (Pechersky 2003). The connection between plate tectonics and the geomagnetic reversal frequency was shown in Petrelis et al. (2011).
Reduction of the magnetic moment during the reversal process (by 5-10 times) increases proportionally the cosmic rays flux reaching the Earth, dramatically affecting the conditions for the existence of all life on the Earth. This is consistent with some evidence of connection of reversals with the geological eras, reflecting major changes in the Earth’s biosphere. In particular, this refers to the boundary of Riphean and Paleozoic (Chizhevsky 1976).
6 CONCLUSIONS
In this work we attempted to explain the generation and cyclic alternation of the magnetic field sign based on the hydromagnetic dynamo theory within the framework of global geodynamic model. Two main acting physical forces of this process are cooling of the originally molten body and internal heating. Cyclic changes of the Earth’s radius occur due to crystallization of the planet from the surface and heating, accompanied by shrinkage and increase in volume, respectively. Conservation of angular momentum leads to the difference in the angular velocities of the mantle, liquid and solid cores. In this case, vortex flows of an electrically conducting liquid are formed in the outer core, resulting in a geomagnetic field generation. The change in the relative rotation of the shells leads to a change in the sign of the geomagnetic field. Faster mantle rotation relative to the outer core produces the direct field, whereas core’s faster rotation results in the reversal field. This picture is supported by experimental studies of the spherical Couette flows. The relationship between the geomagnetic field inversion processes and activation of geodynamic processes and changes in the biosphere is shown.
REFERENCES
Avsyuk Yu.N., 1996. Tidal Forces and Natural Processes, OIFZ RAS, Moscow, 186.
Bobryakov A.P., A.F. Revuzhenko, and E.I.Shemyakin, 1991. Tidal deformation of planets: the experience of experimental modeling, Geotectonics 6, 21-35.
Bott M., 1974. The interior of the Earth.-M.: Mir, 1974. 373.
Braginsky S.I., 1982. Analytical description of secular variations of the geomagnetic field of past centuries and the Earth’s rotation speed, Geomagnetism and Aeronomy 22, 115-122.
Braginsky S.I., 1987. Waves in a stably stratified layer on the Earth’s Core, Geomagnetism and Aeronomy 28, 476-482.
Chizhevsky A. L., 1976. The Earthly Echo of Solar Storms, oscow, 350.
Chumakov N.M., 2001. Periodicity of the main glacial events and their correlation with the endogenous activity of the Earth, Doklady Earth sciences 379.
Dobretsov N.L., A.G. Kirdyashkin, and A.A. Kirdyashkin, 2000. Turbulent convection and magnetic field of the outer core of the Earth, Problems of global geodynamics, Geos.
Dobretsov N.L., A.G. Kirdyashkin, and A.A. Kirdyashkina, 2005. Parameters of hot spots and thermochemical plumes, Russian Geology and Geophysics 6, 575-588.
Dolzhansky F.V., and D.Yu. Manin, 1993. Stability of quasi-two-dimensional shear and jet flows of a rotating fluid, Nonlinear waves, Nauka, Moscow,165-172.
Gaffin S., 1989. ”Analysis of scaling in the geomagnetic polarity reversal record”. Physics of the Earth and Planetary Interiors 57, 284–289.
Hubbard W., 1984. Planetary Interiors, Van Nostrand Reinhold, New York
Josef D., 1976. Stability of fluid motions II, Springer Tracts in Natural Philosophy.
Kalinin Y.D., and V.M. Kisilev, 1978. Unevenness of the daily rotation of the Earth and solar activity: Preprint No. 20, Izmiran, Moscow, 32.
Khain V.E., 2000. Large-scale cyclicity in the tectonic history of the Earth and its possible causes, Geotectonics 6, 3–14.
Khain V.E. Earth is a unique planet of the solar system, 2003. Herald of the Russian Academy of Sciences 73 (9), 822–829.
Kosygin Yu.A., and L.A. Maslov, 1989. On the physical fields of rotating planets, Geotectonics 1, 8–11.
Krymov V.A., 1987. Stability and supercritical regimes of quasi-two-dimensional shear flows in the presence of external friction, Fluid Dynamics 2, 12–18.
Letnikov F.A., 2001. To the problem of the source of internal heat, Doklady Earth sciences 378, 337–389.
Levin B.V., 1996. Role of movements of the inner core of the Earth in tectonic processes, Earth core as a source of anomalies in the gravitational and magnetic field of the Earth and geodynamic effects, Analog, Moscow State University, 444–451.
Lyubimova E.A., 1968. Thermal of the Earth and the Moon, Nauka, Moscow, 278.
Marov M.Ya., 1986. Planets of the solar system, Moscow, Nauka, 320.
Merrill Ronald T., McElhinny Michael W., McFadden Phillip L., 1998). The magnetic field of the earth: paleomagnetism, the core, and the deep mantle. Academic Press.
McElhinny Michael W., McFadden Phillip L., 2000. Paleomagnetism: Continents and Oceans. Academic Press.
Munson B.R., 1975. J.Fluid Mech. 69, 705.
Nadai A., 1969. Plasticity and Destruction of Solid Bodies, 2, Izd-vo Inosr. Liter., Moscow.
Orlenok V.V., 2000. Fundamentals of geophysics, Kalin. Univ., Kaliningrad, 446.
Pechersky D.M., 1997. Some characteristics of the geomagnetic field for 1700 million years, Izv. Earth Phys. 5, 3–20.
Pechersky D.M., 2003. Inversion of the geomagnetic field, plumes and changes in the organic world in the Phanerozoic: amazing coincidence, Izv. Earth Phys. 1, 53–56.
Petrelis F., J. Besse, and J.-P. Valet, 2011. Plate tectonics may control geomagnetic reversal frequency, Geophys, Res. Lett. 38, L19303.
Petrov O.V., and I.B. Movchan, 2003. Self-similarity and dimension in dissipative structuring, Regional geology and metallogeny 19, 33–47.
Petrova G.N., 2002. Cyclic changes in the Earth’s magnetic field, Izv. Earth Phys. 5, 5–14.
Ringwood A.E., 1966. Chemical evolution of the terrestrial planets, Geochim. Cosmochim. Acta 30, 41–104.
Romashov A.N. and S.S. Tsygankov, 1996. In search of a general geotectonic concept, Geotectonics 4, 3–12.
Scheidegger A. E., 1982. Principles of geodynamics, Third, Completely Revised Edition, Springer-Verlag, New York, 384.
Smyslov A.A., et al., 1979. The thermal regime and radioactivity of the Earth, Leningrad, 191.
Tkalčić H., M. Younget, T. Bodin, S. Ngo and M. Sambridge, 2013. The shuffling rotation of the Earth’s inner core revealed by earthquake doublets, Nature Geoscience 6, doi:10.1038/ngeo1813.
Tsygankov S.S., S.S.Tsygankov (II), and S.S. Tsygankov (III), 2003. The design of the spaceship ”Planet Earth”, Priroda 6, 70–79.
Tsygankov S.S., 2006. On the possible mechanism of inversion of the magnetic field, Doklady Physics 51 (7), 393–396.
Tsygankov S.S., 2009. On the possible mechanism of the generation and reversal of the geomagnetic field, Fiz. mezomekh 12 (3), 101.
Vorobiev A.A., 1980. Equilibrium and transformation of energy types in the bowels, Tomsk, TSU Press, 211.
Wetherill G.W., 1972. The beginning of continental evolution, Tectonophysics 13, 31–45.
Windley B.F. ed., 1975. The Early history of the Earth, A Wiley Interscience Publication.
Yavorska I.M., Yu.N. Belyaev, and A.A. Monakhov, 1977. Investigation of stability and secondary flows in rotating spherical layers for arbitrary Rosbi numbers, Doklady Physics 237 (4), 804–807.
Yavorska I.M., N.M. Astafieva, and Vvedenskaya N.D., 1978. On the stability and nonuniqueness of fluid flows in rotating spherical layers, Doklady Physics 241 (1), 52–55.
Yavorsky B.M., and Detlaf A. A., 1977. Handbook of Physics, Nauka, 942.
Zharkov V.N., 1983. The internal structure of the Earth and the planets, Nauka, Moscow, 406.